Mathematica 10
Statistical Distribution Examples

Multivariate continuous and discrete parametric distributions.

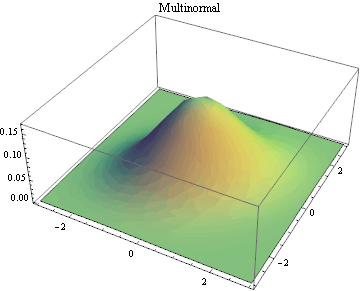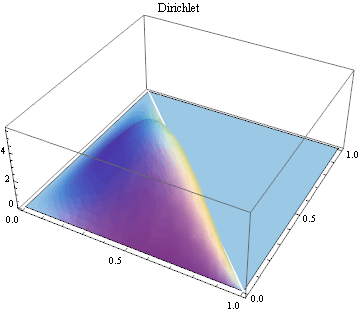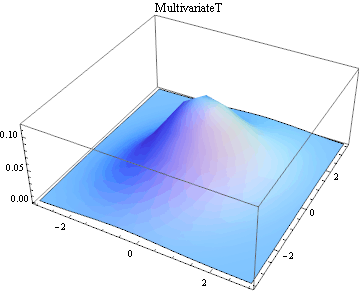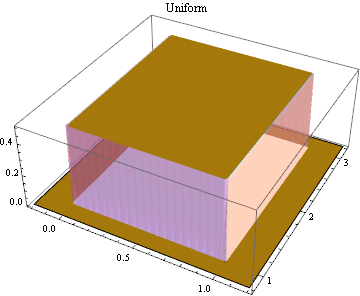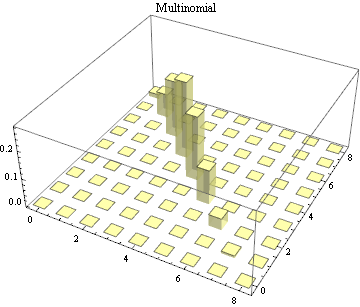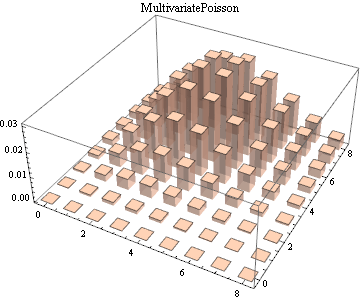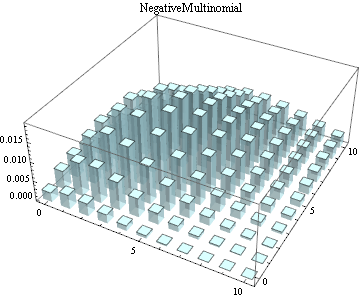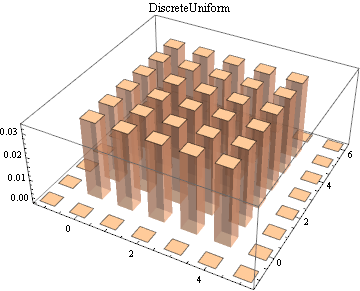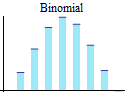
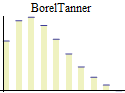
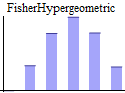
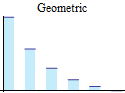
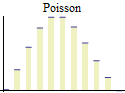
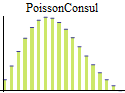
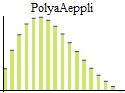
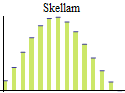
Discrete univariate parametric distributions

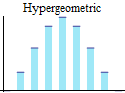
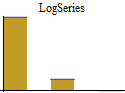
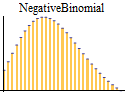
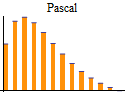
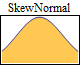
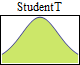
Univariate continuous parametric distributions

An extensive list of properties can be queried for each supported distribution

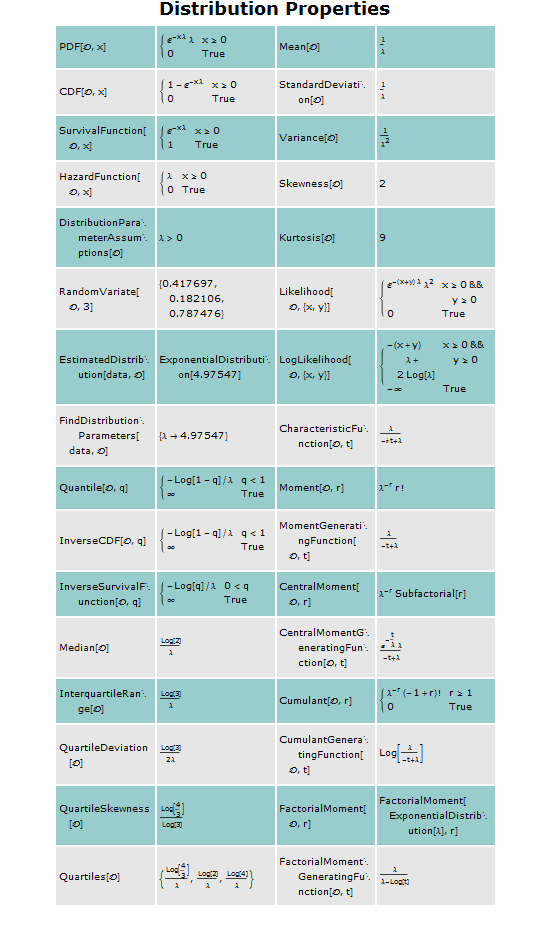
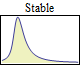
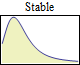
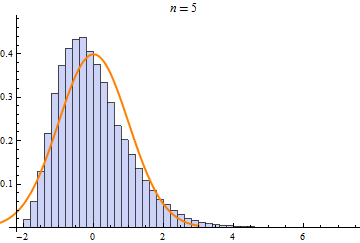
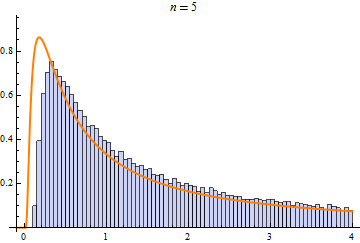
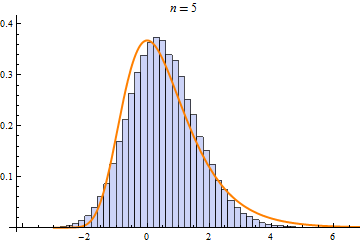
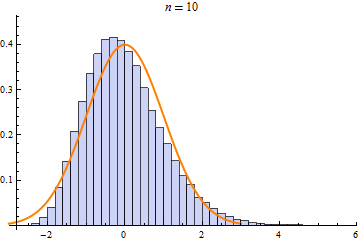
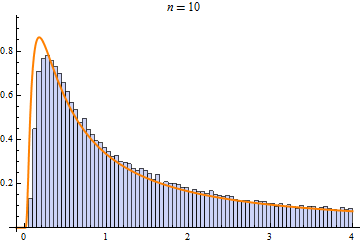
Some operations, such as sum, min, or max of random variables, converge to only a few limit distributions when repeated. These limit distributions include NormalDistribution, StableDistribution, MinStableDistribution, and MaxStableDistribution

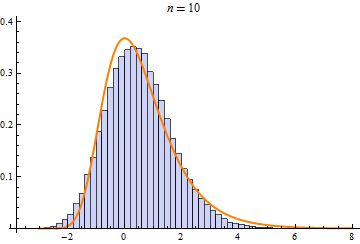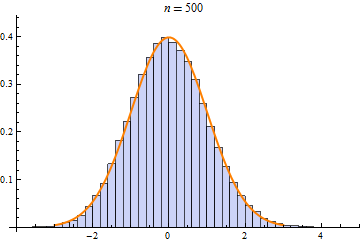
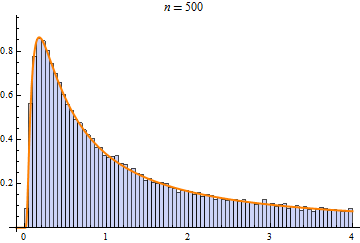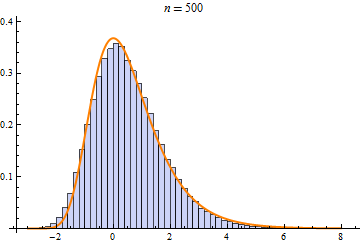NormalDistribution	StableDistribution	MaxStableDistribution

Simulate Incomes with Dagum Distribution

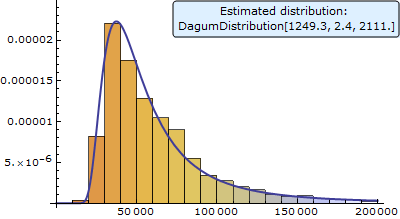
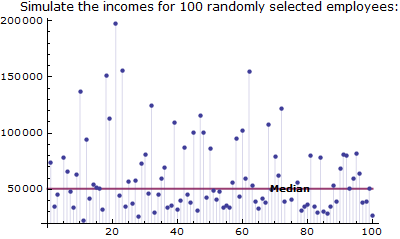
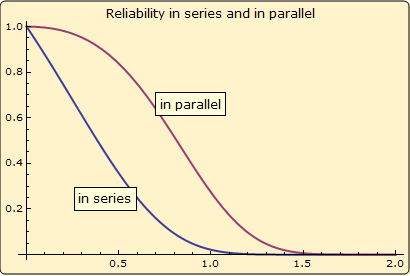
Model a lifetime of a device by a GompertzMakehamDistribution and compare reliability of systems composed of two such devices put in series or in parallel.

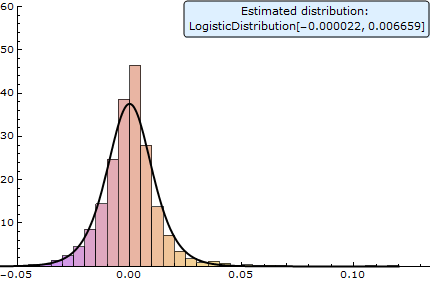
Use Logistic Distribution to Simulate Fractional Change
LogisticDistribution provides a very good fit for fractional price changes from the previous closing price of stocks. Use EstimatedDistribution to find best fit with logistic distribution for the daily fractional price changes of Standard & Poor’s 500 index from January 1, 2000 to January 1, 2009. Then use this distribution to run a simulation.

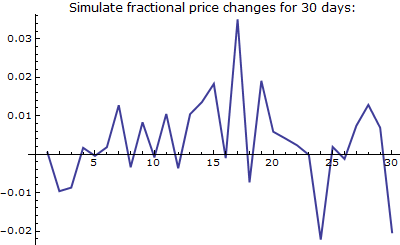
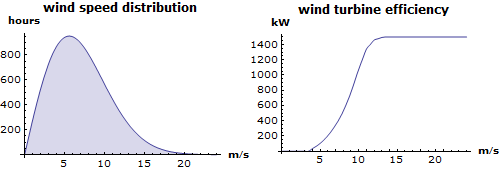
More various examples

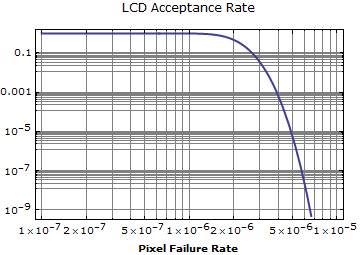
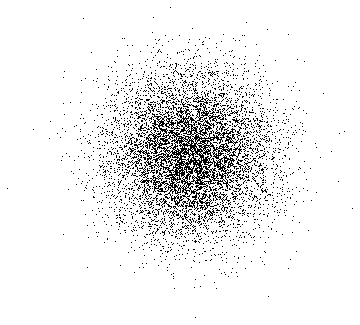
Gauss Normal distribution

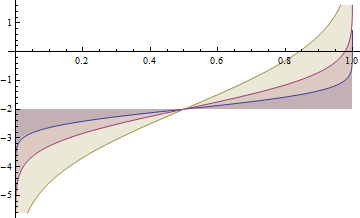
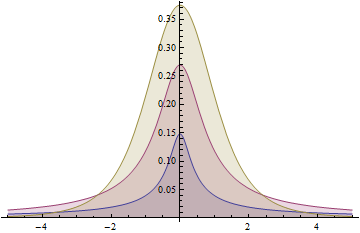
Student distribution

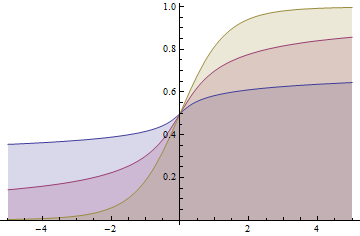
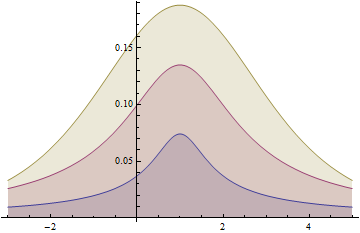
Examples of 3D-Plotting

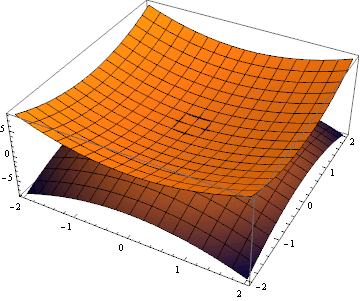
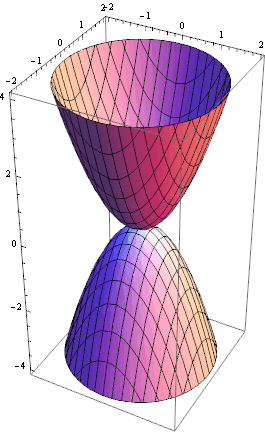
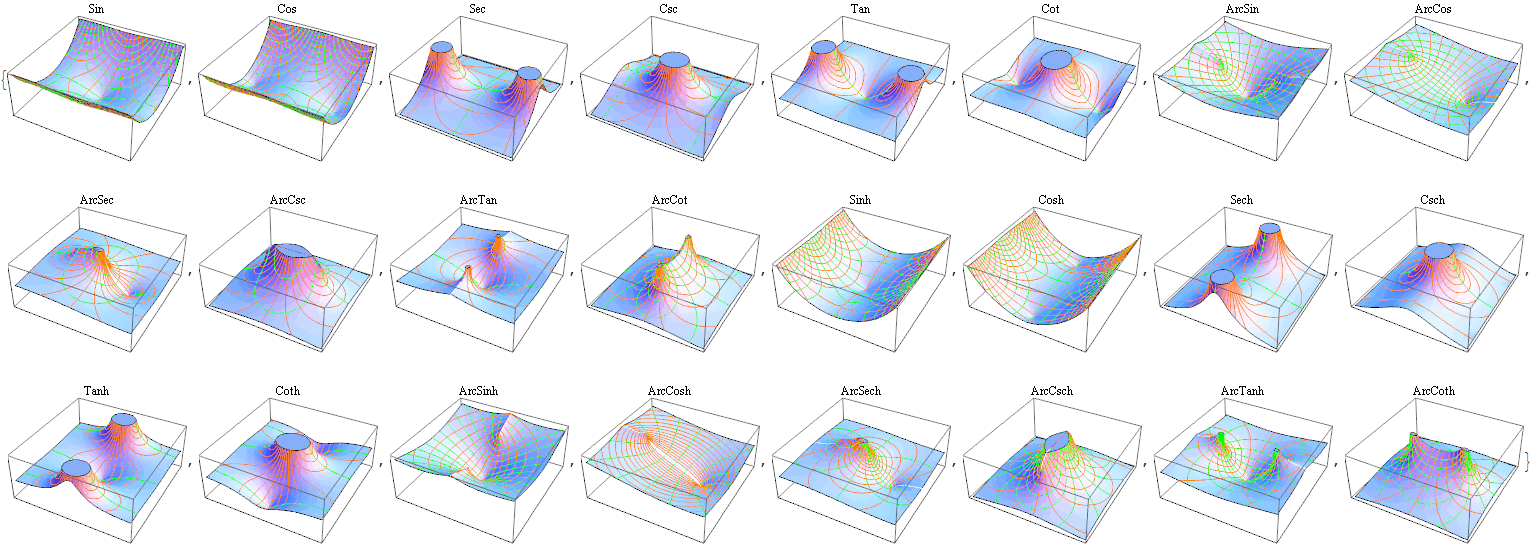
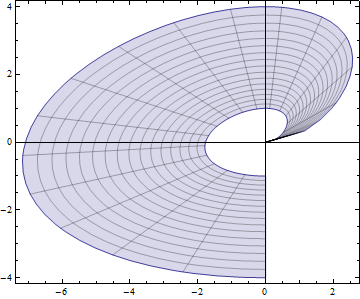
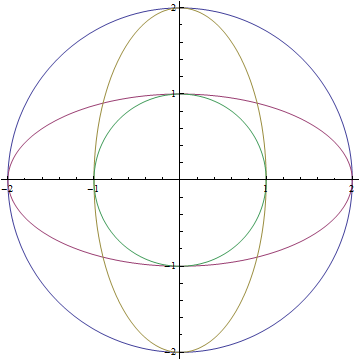
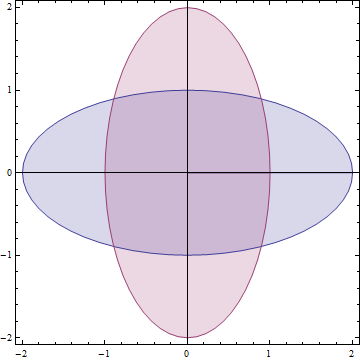
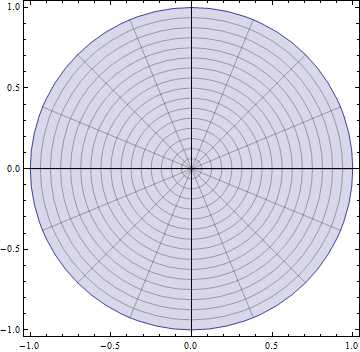
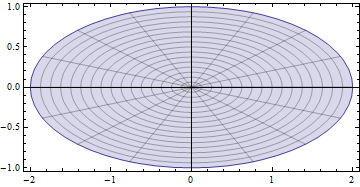
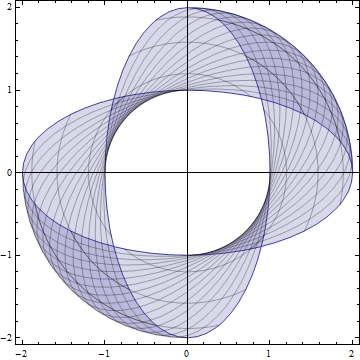
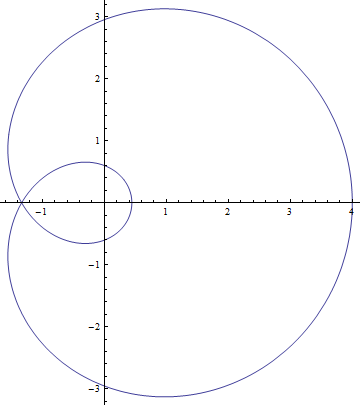
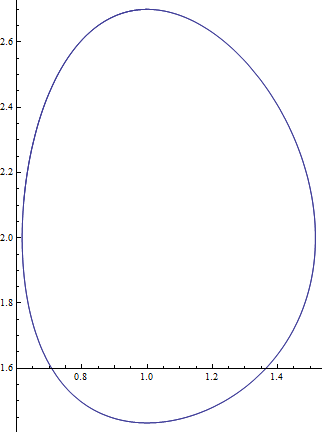
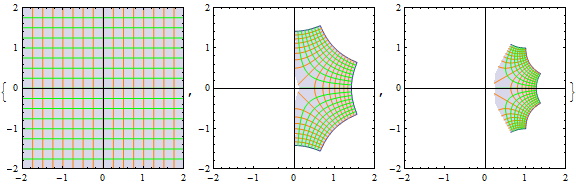
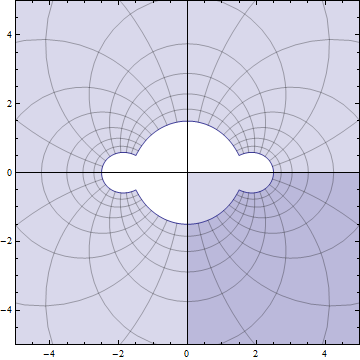
Parametric Plotting

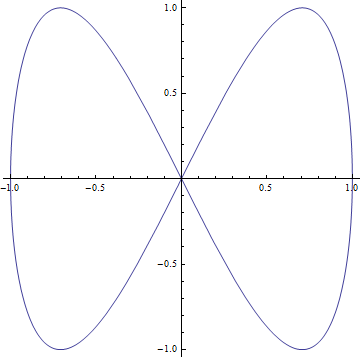
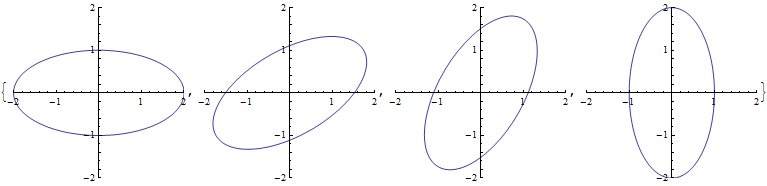
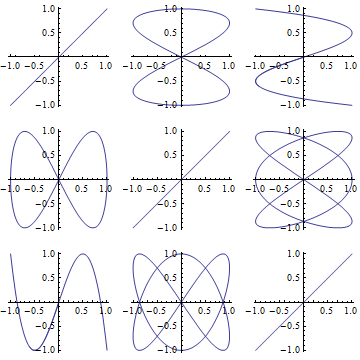
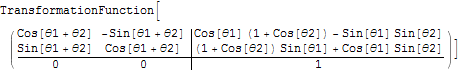
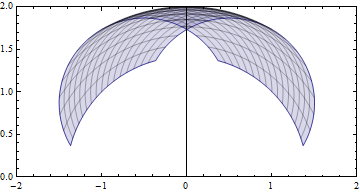
Parametric 3D-Plotting

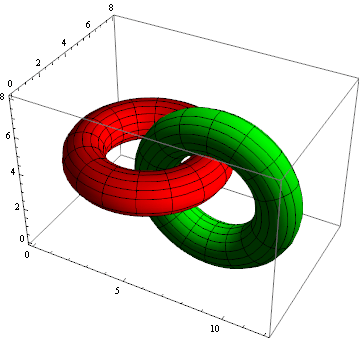
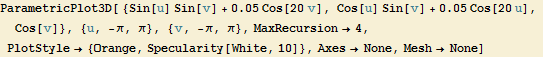
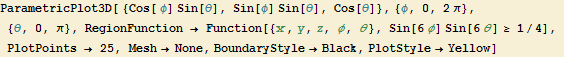
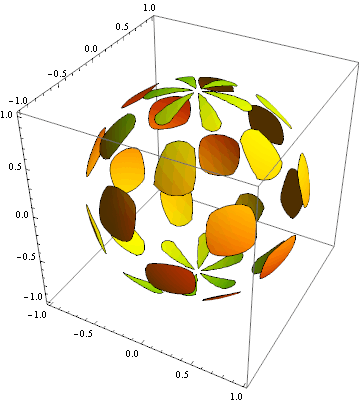
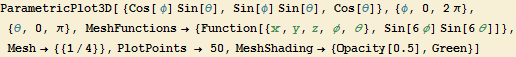
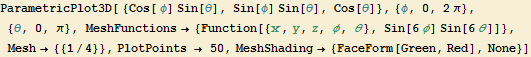
For more information and examples visit   http://www.wolfram.com

For how to learn and teach math see the video with Conrad Wolfram Talk at
Wolfram Technology Conference 2010:

http://www.computerbasedmath.org/resources/reforming-math-curriculum-with-computers.html